Transformers efficiently transfer electrical energy from one circuit to another by means of magnetic induction. Each phase of a transformer is composed of two separate coil windings wound on a common core.
The transformer’s primary winding receives electrical energy from the power source. When the primary winding is energized with an alternating current (AC), alternating magnetic lines of force, called “flux,” circulate through the core, establishing a magnetic field.
With a second winding wrapped around the same core, a voltage is induced by the magnetic field. This winding is called the secondary winding. The amount of voltage induced in each turn of the secondary winding will be the same as the voltage across each turn of the primary winding; this is referred to as the transformer turns ratio.
If the secondary winding has fewer turns than the primary, a lower voltage will be induced in the secondary. This type of transformer is called a step-down transformer.
A secondary coil with twice as many turns as the primary will be cut twice as many times by the magnetic flux, and twice the applied primary voltage will be induced in the secondary. This transformer is known as a step-up transformer.
Note: The primary is always connected to the source of power, and the secondary is always connected to the load. Either the high- or low-voltage winding can be the primary or the secondary.
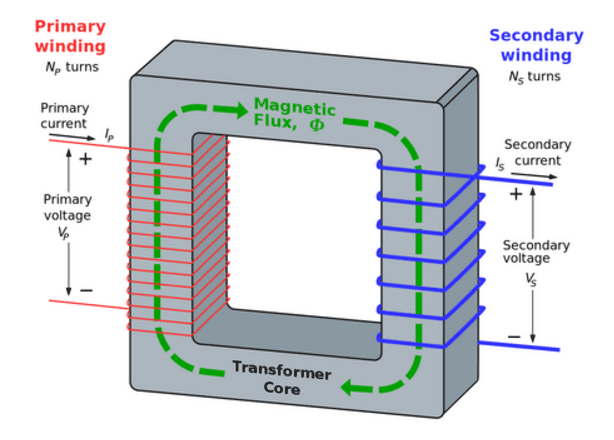
When the primary winding of a transformer is energized with an alternating current (AC), alternating magnetic lines of force, called “flux,” circulates through the core, establishing a magnetic field. Photo: Quora
How TTR is Calculated
The total induced voltage in each winding is proportional to the number of turns in that winding and the current is inversely proportional to both voltage and number of turns.
E1 / E2 = N1 / N2 = I2 / I1
E1 is the primary voltage and I1 the primary current, E2 the secondary voltage and I2 the secondary current, N1 the primary turns and N2 the secondary turns. If voltage is stepped up, the current must be stepped down, and vice versa. The number of turns remains constant unless there is a tap changer.
Example 1
If the primary voltage of a transformer is 110 volts (V), the primary winding has 100 turns, and the secondary winding has 400 turns, what will the secondary voltage be?
E1 / E2 = N1 / N2
110 / E2 = 100 / 400
100 E2 = 44,000
E2 = 440 Volts
Example 2
If the primary current is 20 amps, what will the secondary current be?
E2 x I2 = El x I1
440 x I2 = 110 x 20 = 2,200
I2 = 5 amps
Since there is a ratio of 1 to 4 between the turns in the primary and secondary circuits, there must be a ratio of 1 to 4 between the primary and secondary voltage and a ratio of 4 to 1 between the primary and secondary current.
As voltage is stepped up, the current is stepped down, keeping volts multiplied by amps constant. This is referred to as “volt-amps.”
Calculate the ratio of each three-phase winding based on the line-to-neutral voltage of the wye winding. Divide the line-to-line winding voltage by 1.732 to obtain the correct line-to-neutral voltage.
Example: 13200-480Y/277 would be 13200/277 = 47.653
Check the tap changer position to make sure it is set where the nameplate voltage is based. Otherwise, the turns ratio test information cannot be compared with the nameplate.
How TTR is Measured
The turns ratio test is capable of detecting shorted turns in the winding, which indicate insulation failure by determining if the correct turns ratio exists. Shorted turns may result from short circuits or dielectric failures.
Measurements are taken by applying a known low voltage across one winding and measuring the induced voltage on the corresponding winding. The low voltage is normally applied across a high-voltage winding so that the induced voltage is lower, reducing hazards while performing the test.
Related: Electrical Shock and Arc Flash PPE Overview
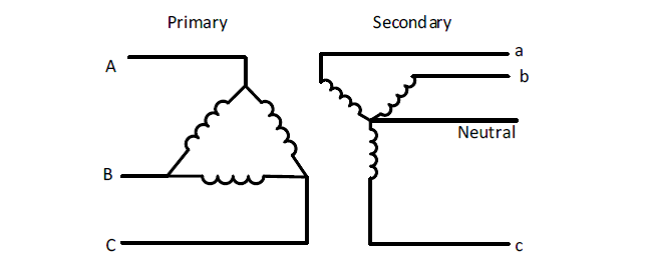
Look at the nameplate phasor diagram to find out what winding on the primary corresponds to a winding on the secondary. Photo: Quora
The voltage ratio obtained by the test is compared to the nameplate voltage ratio. Examine the nameplate phasor diagram to identify which winding on the primary corresponds to a winding on the secondary.
The ratio obtained from the field test should fall within 0.5%, or whichever the manufacturer specifies.
New transformers of good quality typically compare to the nameplate within 0.1%. For three-phase delta/wye or wye/delta connected transformers, a three-phase equivalency test should be performed. The test is conducted and calculated across corresponding single windings.